ggdensity

Improved density visualization in R

---

James Otto, David Kahle

Baylor University

8/7/2022

Introduction

• ggplot2 includes several ways to estimate and visualize densities for uni- and bivariate data
Limited by the difficulty of interpreting density height
ggdensity provides interpretable visualizations via highest density regions

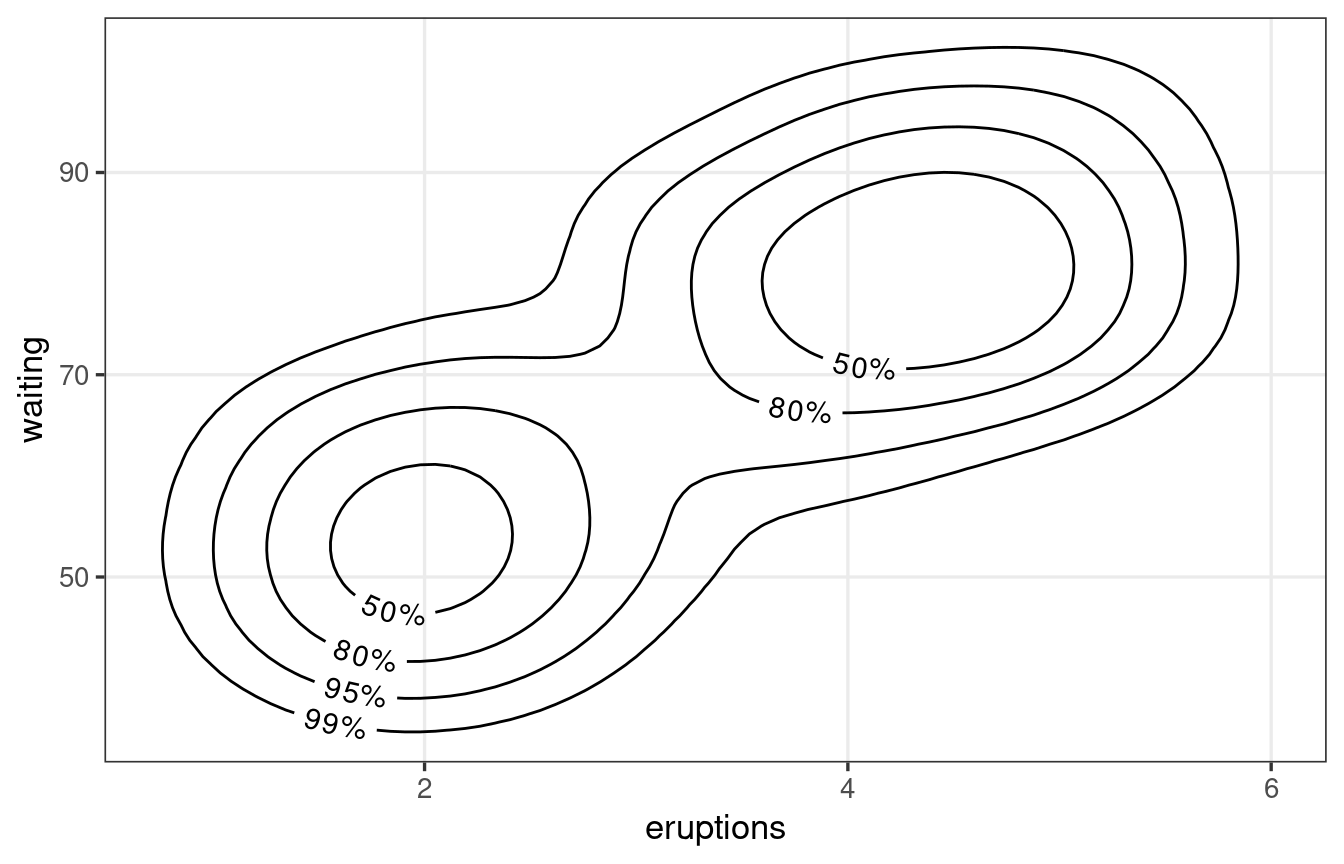
A Motivating Example

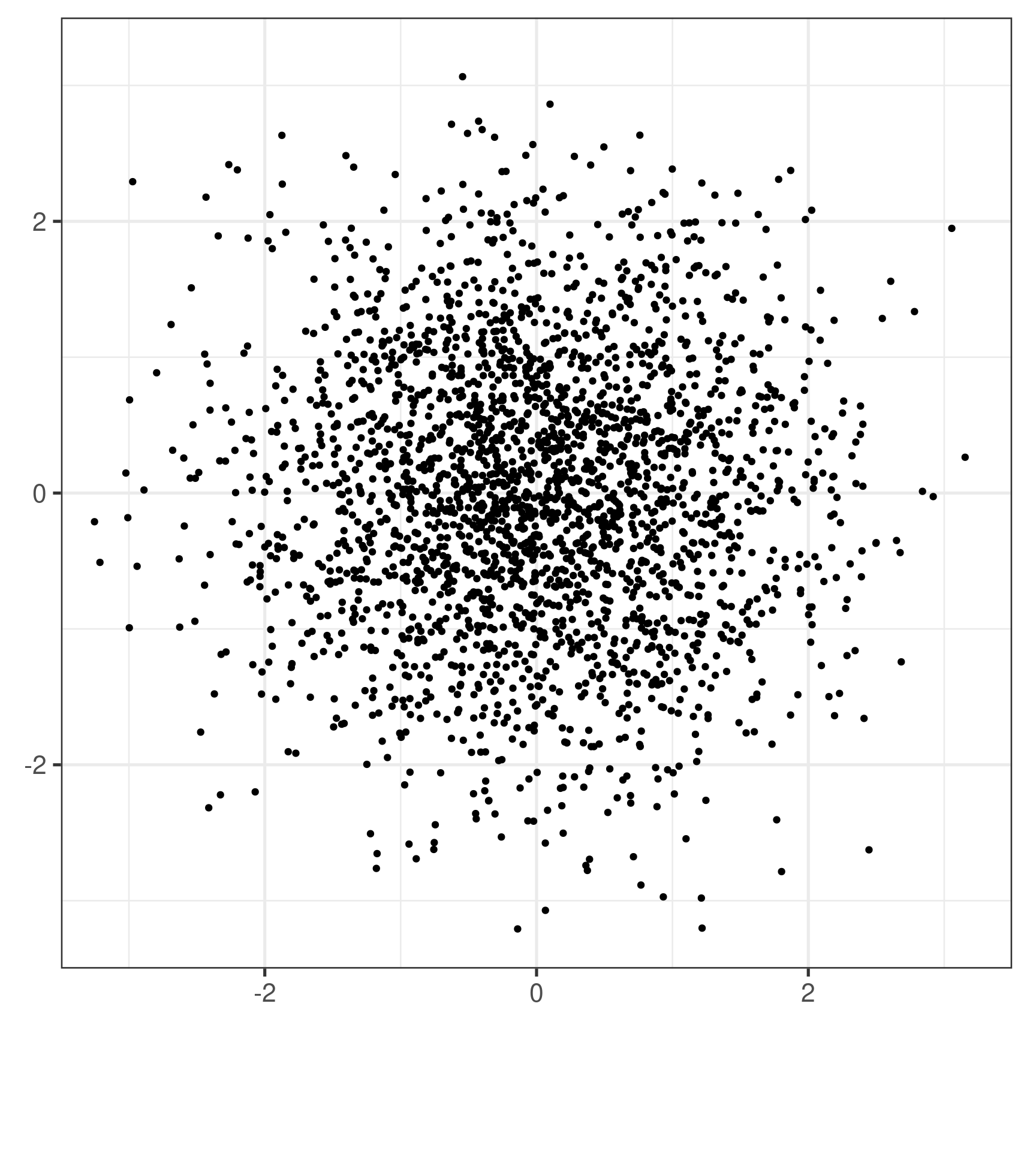
A Motivating Example

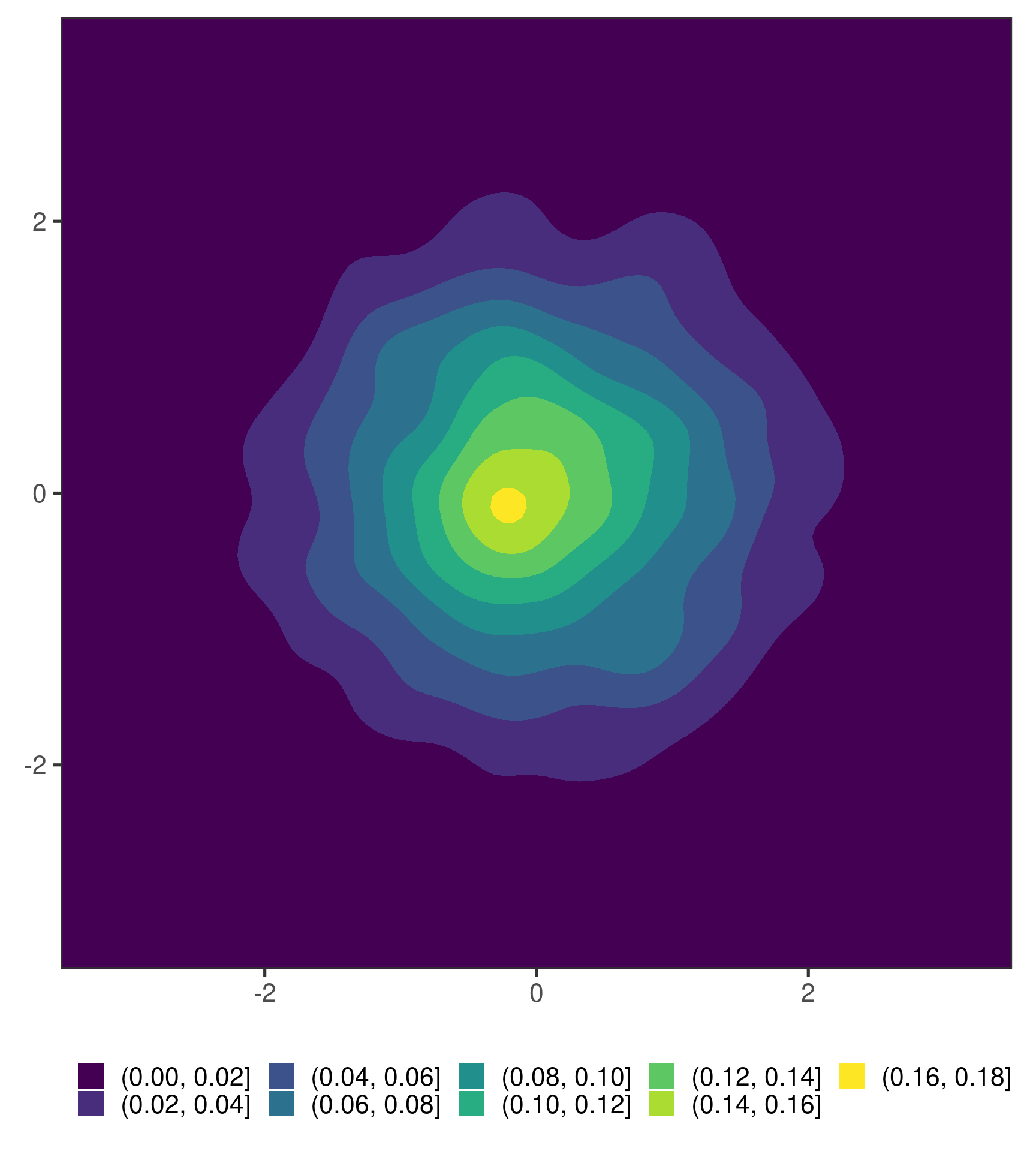
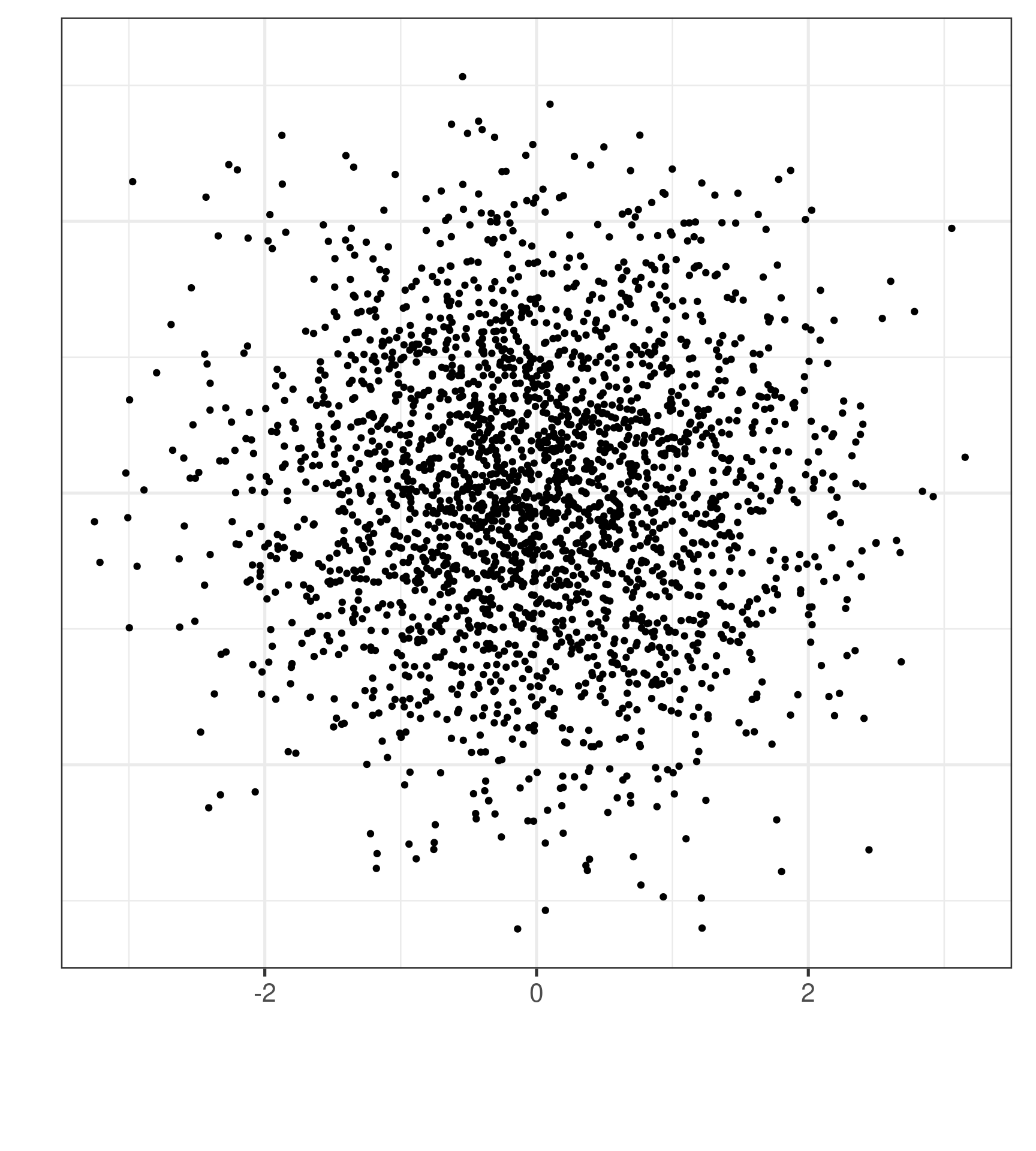
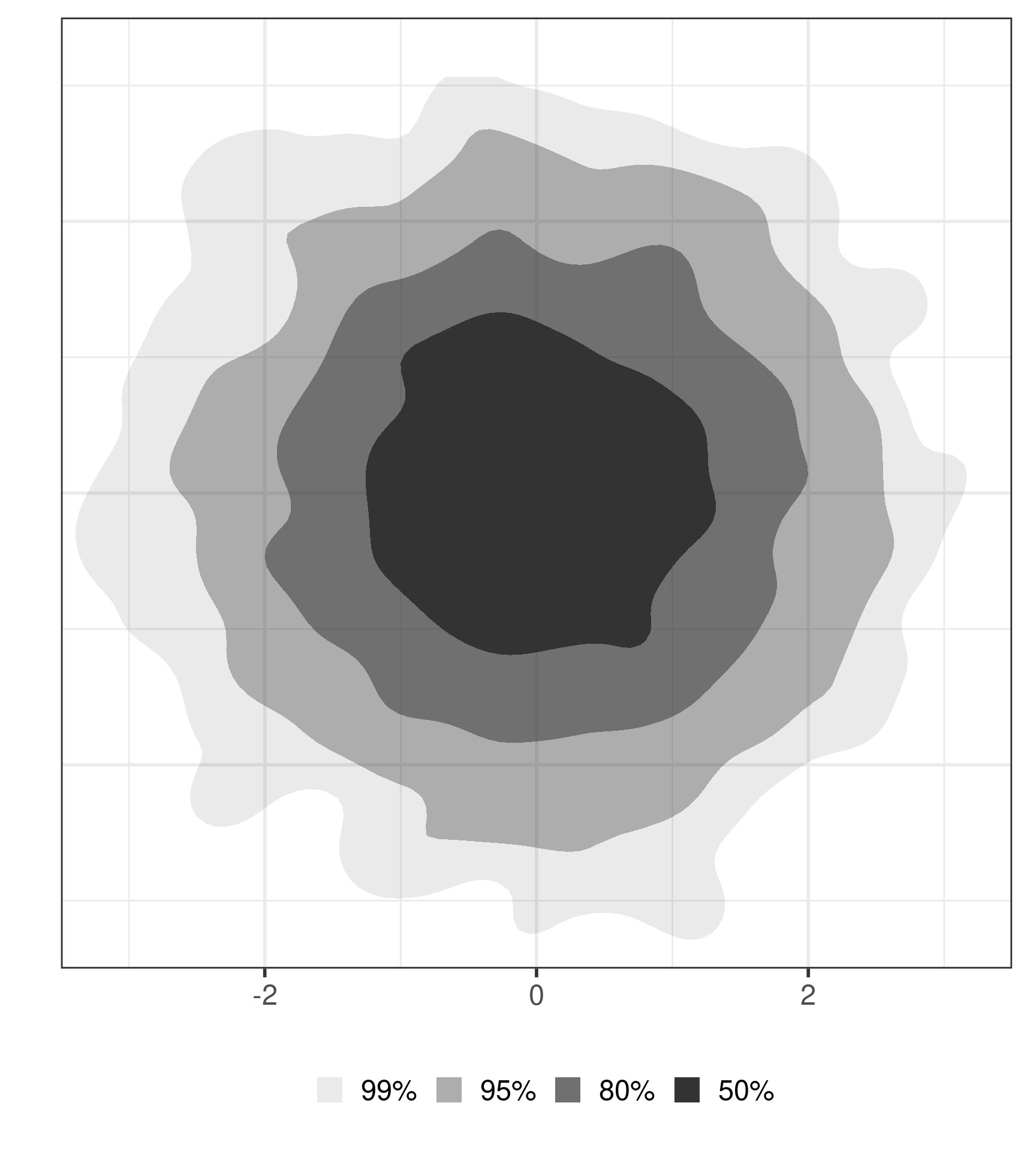
A Motivating Example

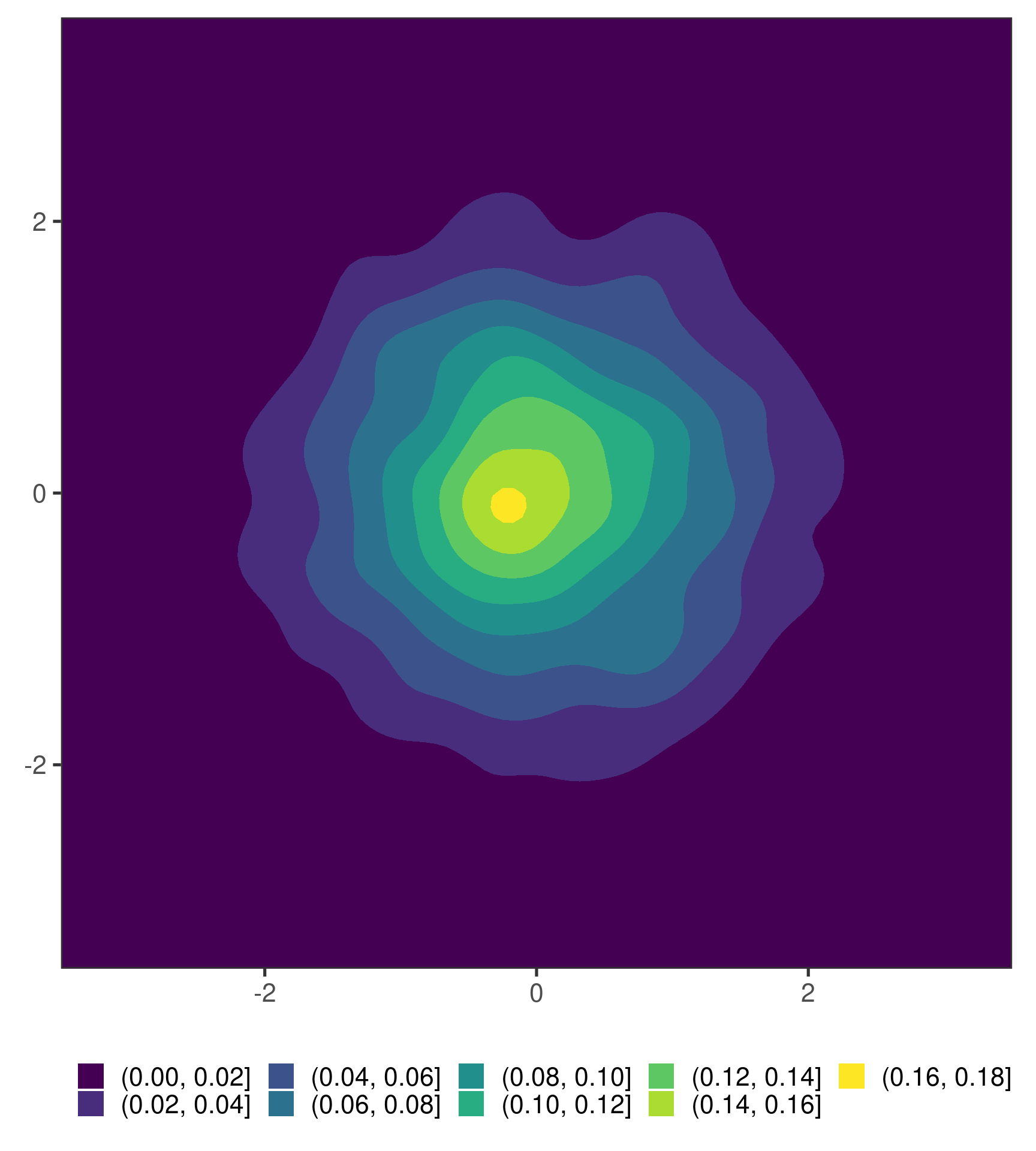
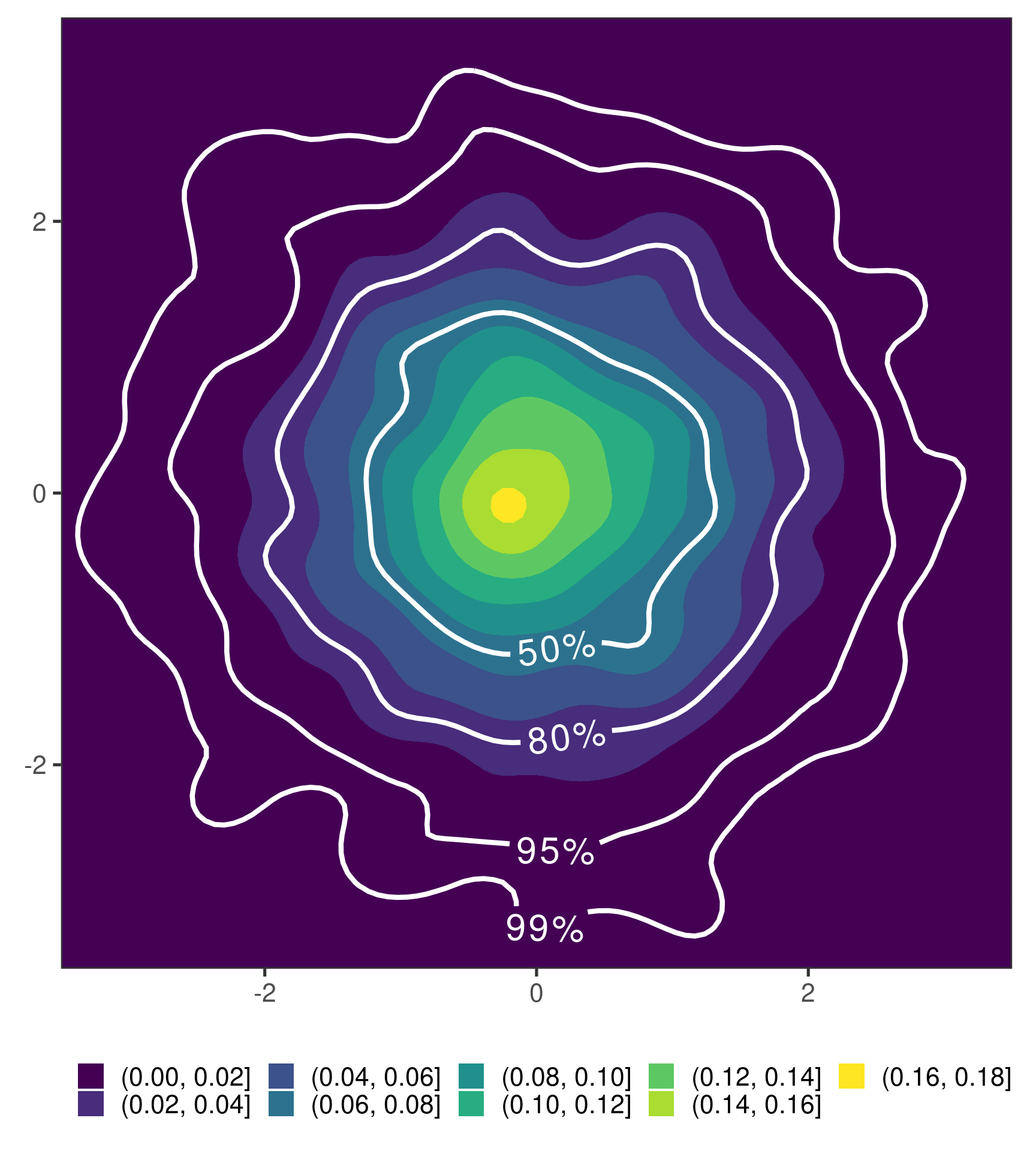
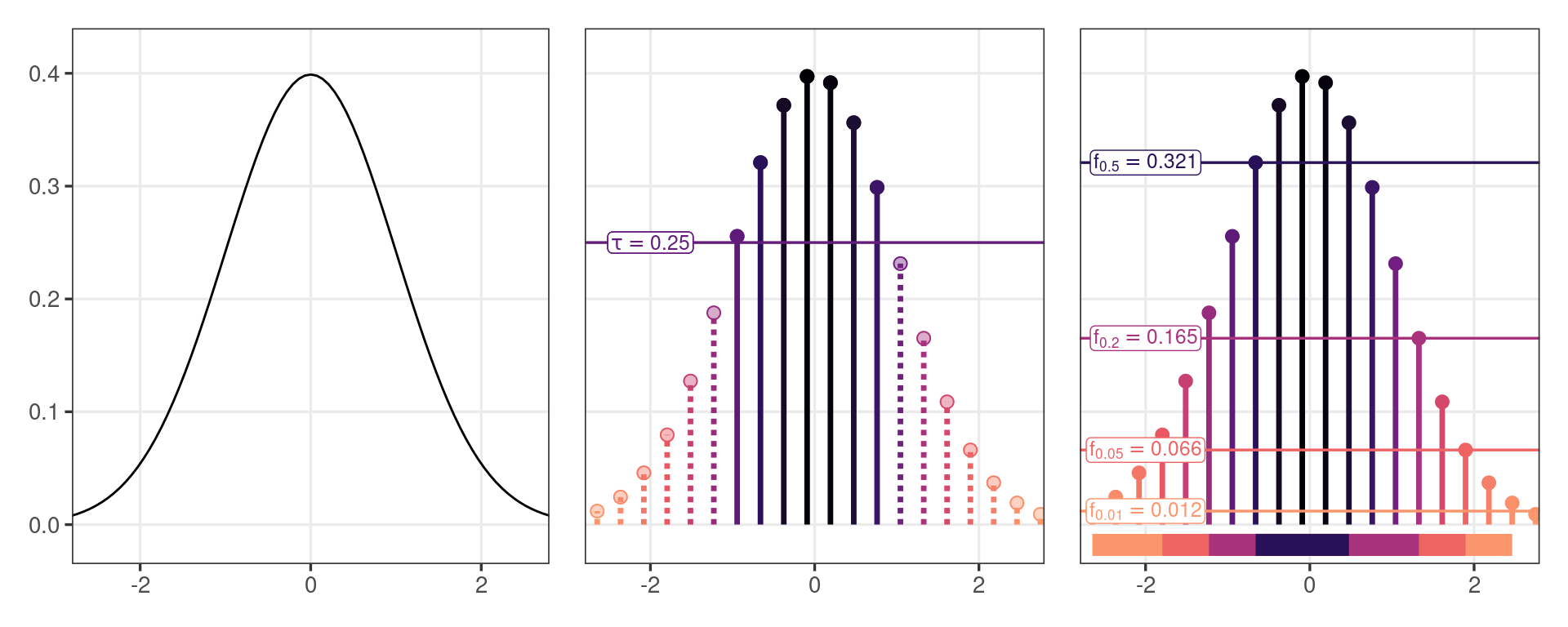
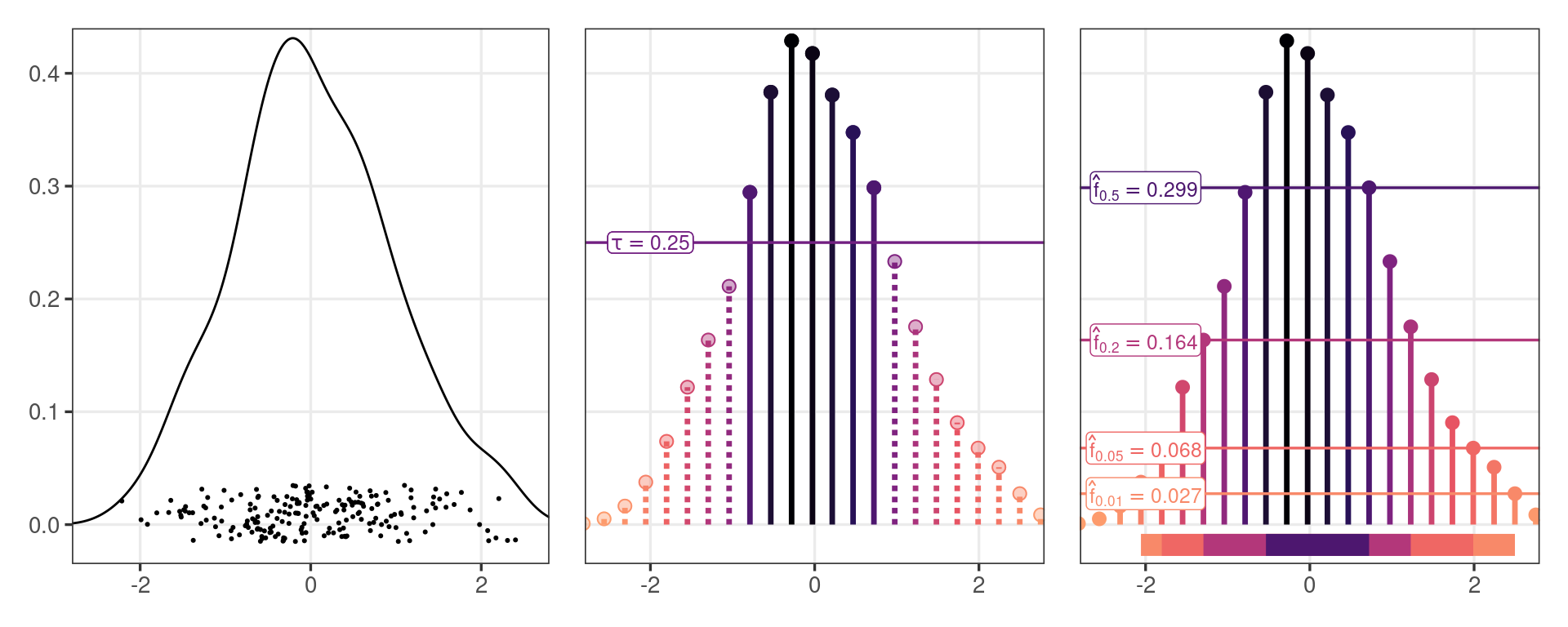
Defining the HDR

Let \(f(x, y)\) be the pdf of a random vector \(\left( X, Y \right) \in \mathbb{R}^2\). Then for \(\alpha \in (0,1)\) the \(100(1 - \alpha)\%\) highest density region (HDR) is the subset \(R(f_{\alpha}) \subset \mathbb{R}^2\) such that \(R(f_{\alpha}) = \{(x, y): f (x, y) \geq f_{\alpha}\}\) where \(f_{\alpha}\) is the largest constant such that \(\mathrm{P}\left[(X, Y) \in R(f_{\alpha})\right] \geq 1 - \alpha\).

Hyndman (1996)

geom_hdr()

df <- tibble(x = rnorm(1000), y = rnorm(1000))

ggplot(df, aes(x, y)) + 
  geom_point()

df <- tibble(x = rnorm(1000), y = rnorm(1000))

ggplot(df, aes(x, y)) + 
  geom_hdr()

df <- tibble(x = rnorm(1000), y = rnorm(1000))

ggplot(df, aes(x, y)) + 
  geom_hdr(
    method = "kde"
  )

df <- tibble(x = rnorm(1000), y = rnorm(1000))

ggplot(df, aes(x, y)) + 
  geom_hdr(
    method = "mvnorm"
  )

df <- tibble(x = rnorm(1000), y = rnorm(1000))

ggplot(df, aes(x, y)) + 
  geom_hdr(
    method = "histogram"
  )

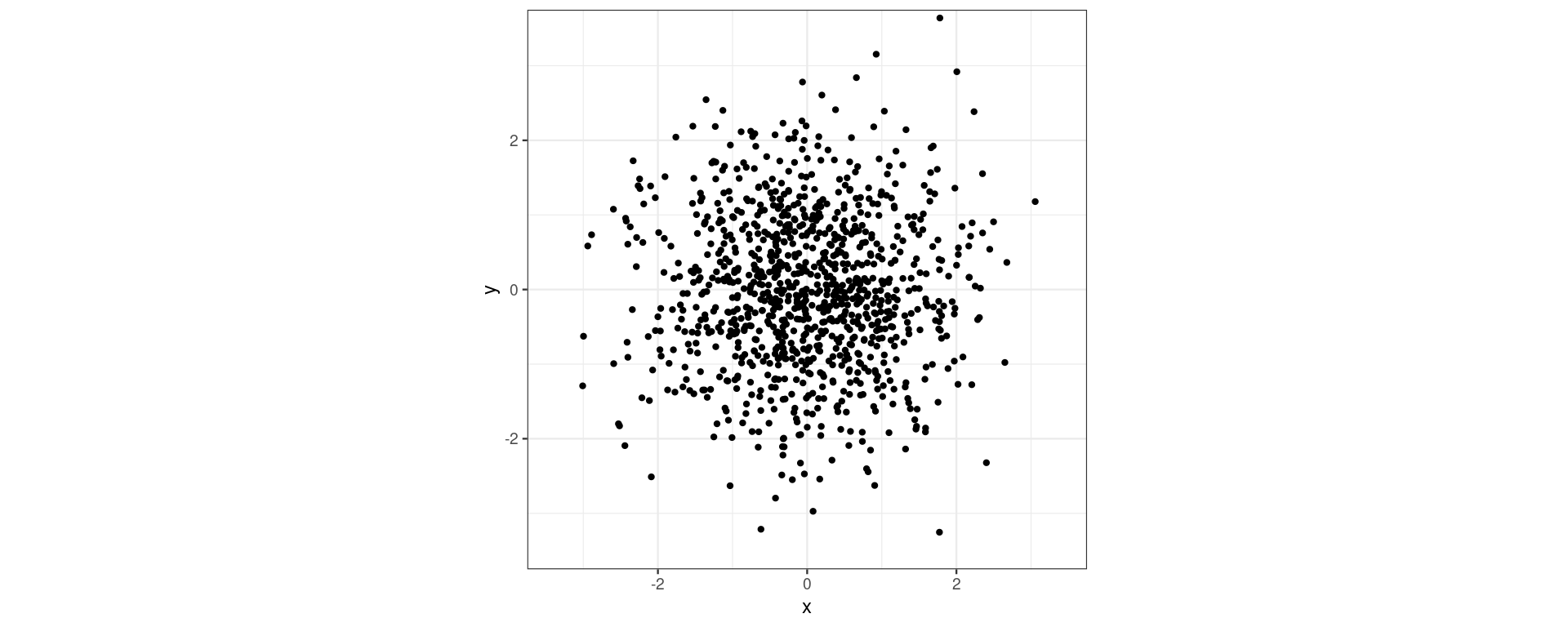
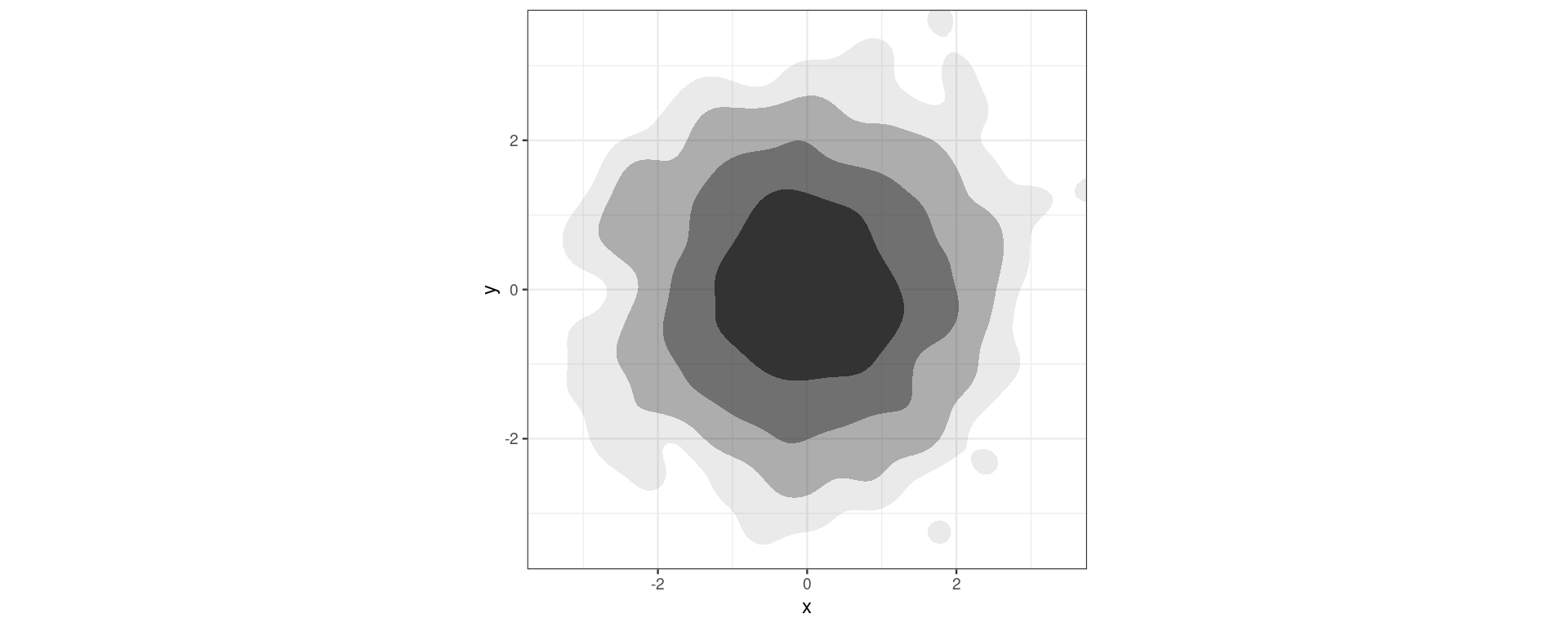
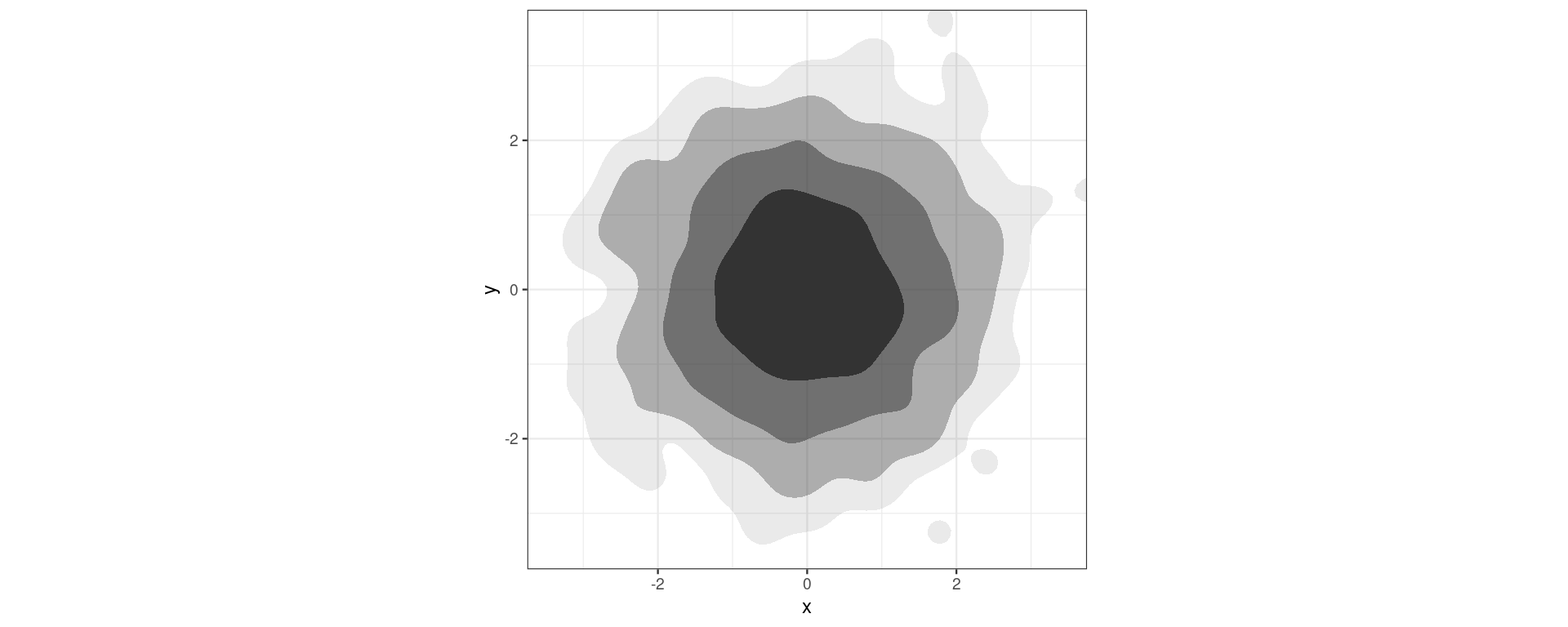
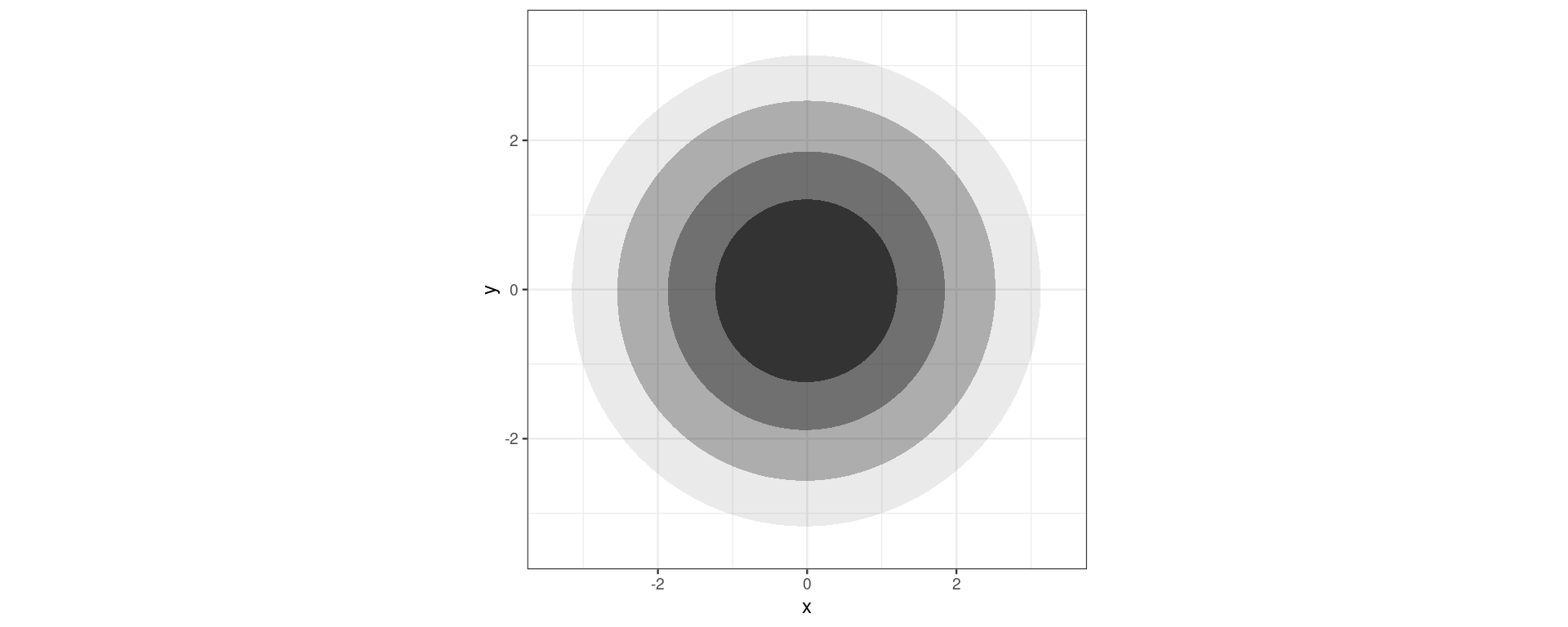
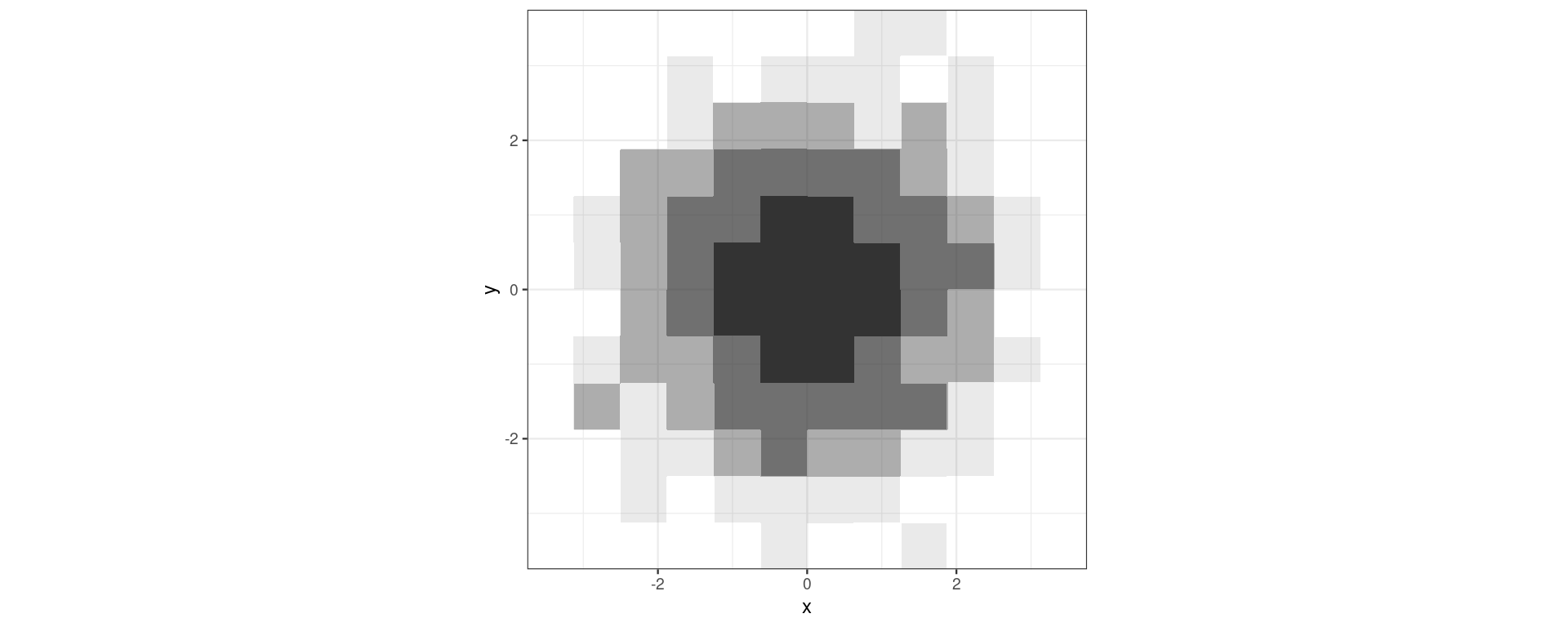
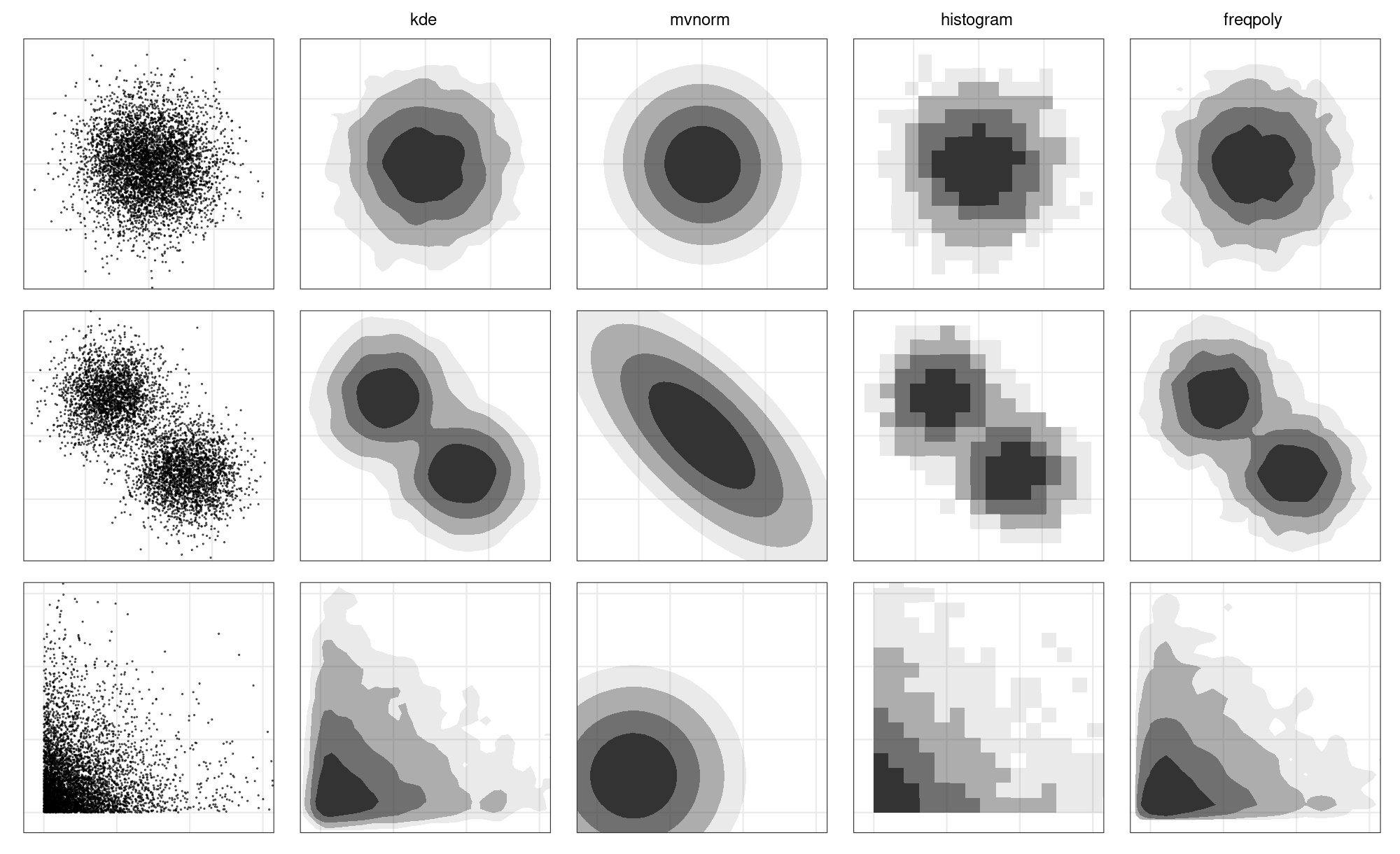
Palmer Penguins

Palmer Penguins

Palmer Penguins

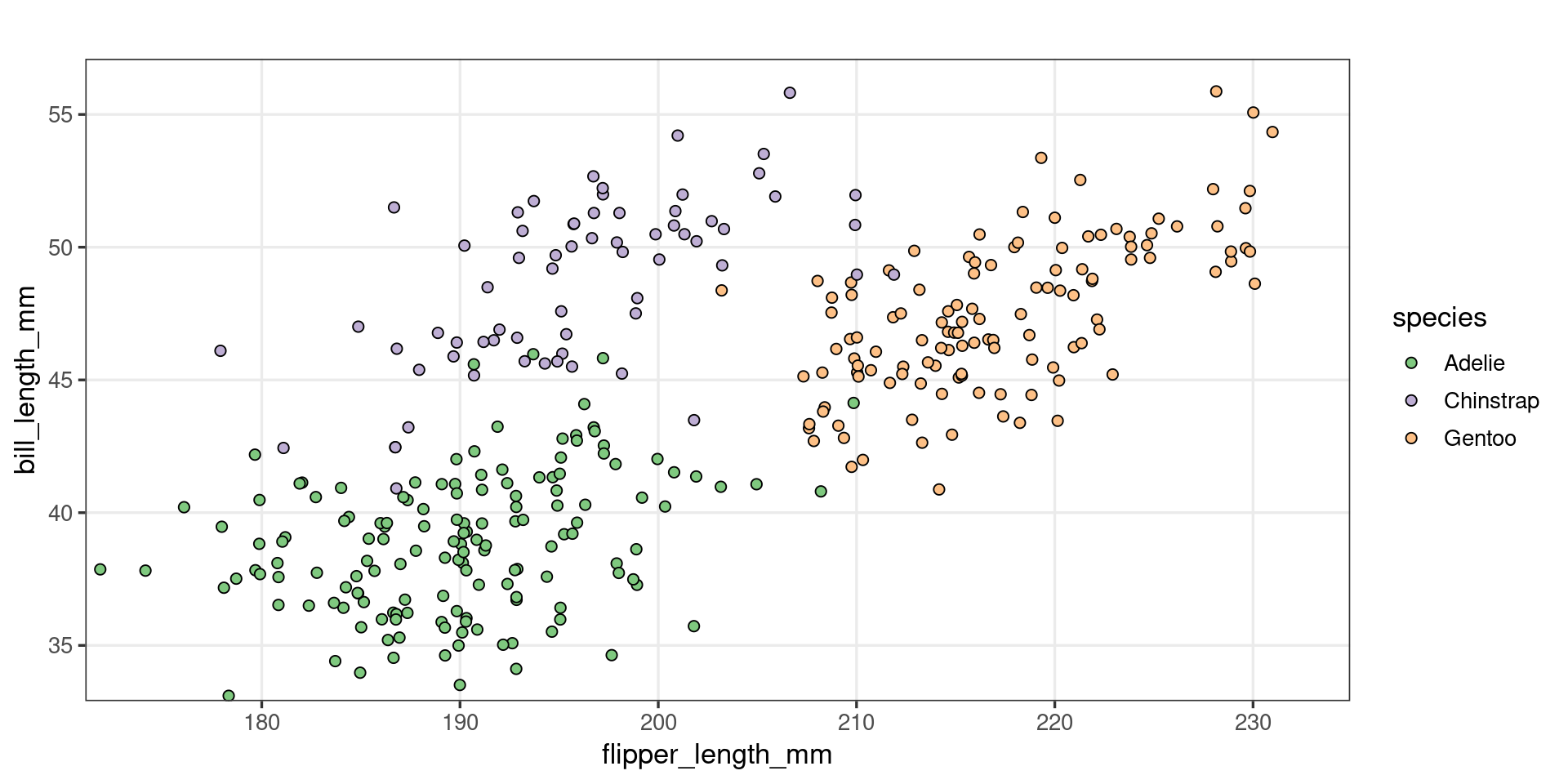
Palmer Penguins

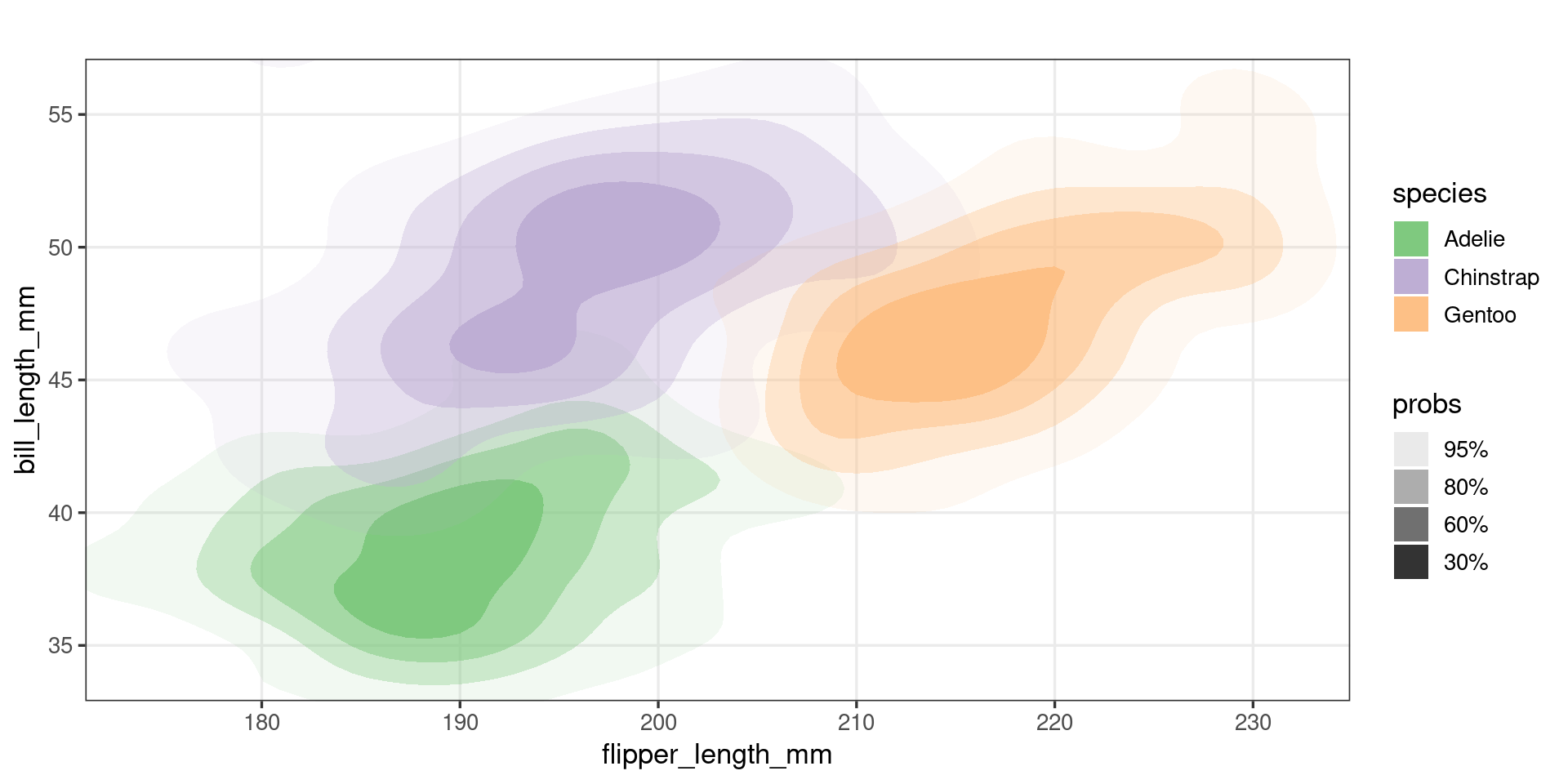
Palmer Penguins

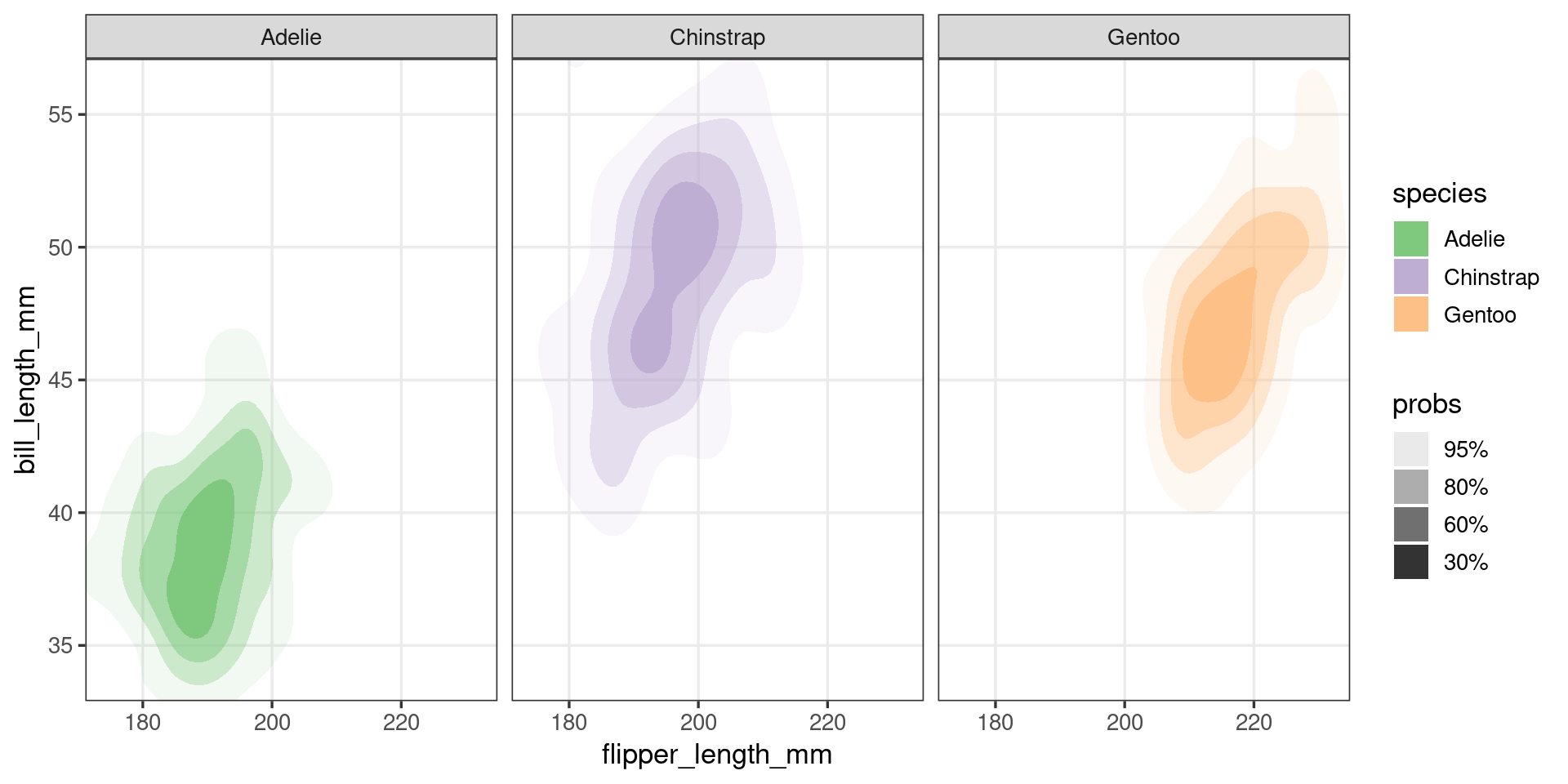
geom_hdr_fun()

f <- function(x, y) dnorm(x) * dgamma(y, 5, 3)

ggplot() +
  geom_hdr_fun(fun = f, xlim = c(-4, 4), ylim = c(0, 5))

df <- data.frame(x = rexp(100, 1), y = rexp(100, 1))

# pdf for parametric density estimate
f <- \(x, y, lambda) dexp(x, lambda[1]) * dexp(y, lambda[2])

# estimate parameters governing joint pdf
lambda_hat <- apply(df, 2, mean)

# make plot
ggplot(df, aes(x, y)) +
  geom_hdr_fun(
    fun = f, args = list(lambda = lambda_hat),
    xlim = c(0, 7), ylim = c(0, 7) 
  ) +
  geom_point(fill = "lightgreen", shape = 21) +
  coord_fixed()

misc. geom’s

p <- ggplot(faithful, aes(eruptions, waiting))

p + geom_hdr_lines()
p + geom_hdr_points()
p + geom_hdr_rug()

p <- ggplot(faithful, aes(eruptions, waiting))

p + 
  geomtextpath::geom_textdensity2d(
    aes(level = after_stat(probs)),
    stat = "hdr_lines", alpha = 1
  )

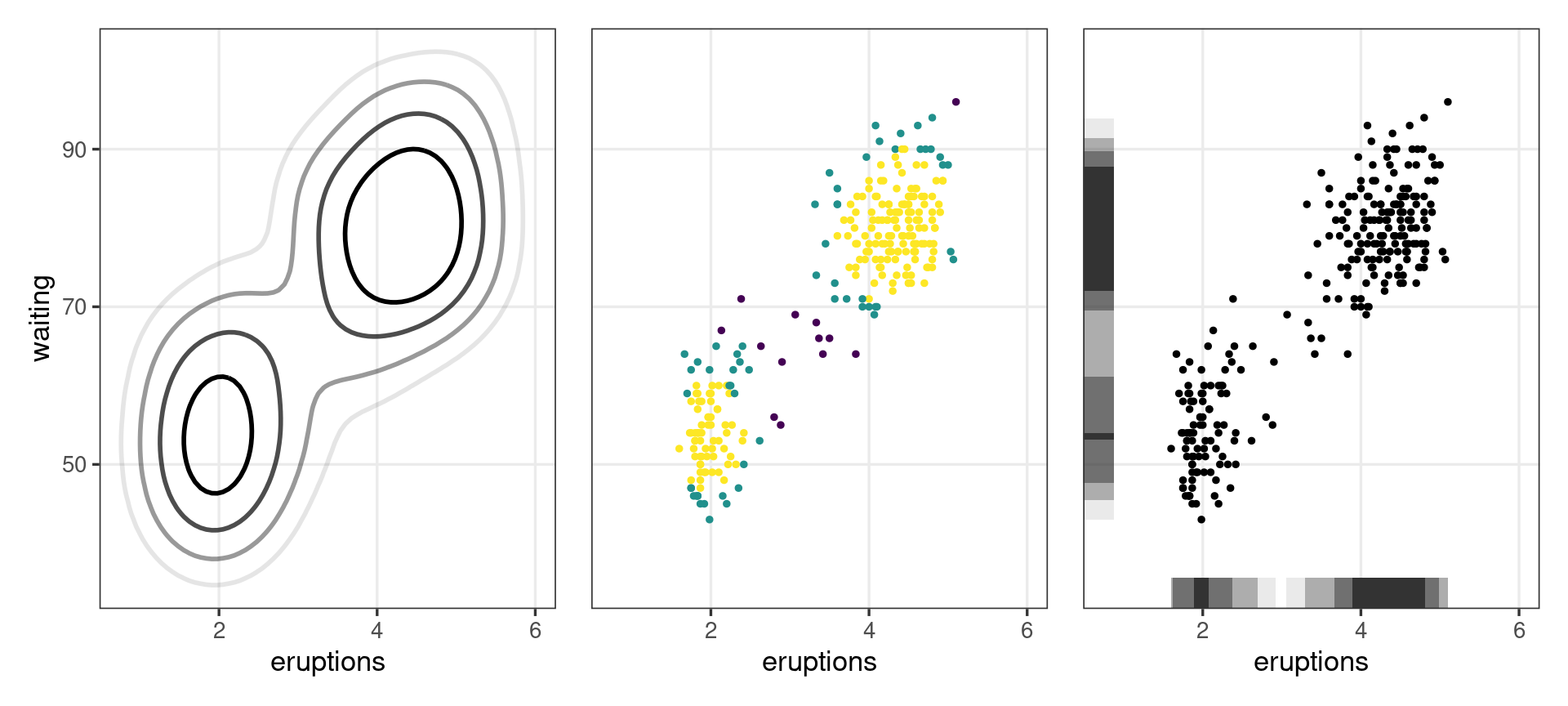
Related Projects

• hdrcde
• gghdr
• ggdist

References

Azzalini A, Bowman AW. 1990. A look at some data on the old faithful geyser. Journal of the Royal Statistical Society. Series C (Applied Statistics) 39: 357–365.

Cameron A, van den Brand T. 2022. Geomtextpath: Curved text in ’ggplot2’.

Horst AM, Hill AP, Gorman KB. 2020. Palmerpenguins: Palmer archipelago (antarctica) penguin data.

Hyndman RJ. 1996. Computing and graphing highest density regions. The American Statistician 50: 120–126.

Plummer M. 2003. JAGS: A program for analysis of bayesian graphical models using gibbs sampling.

Plummer M. 2021. Rjags: Bayesian graphical models using MCMC.

Scott D. 2015. Multivariate density estimation: Theory, practice, and visualization.

Scrucca L, Fop M, Murphy TB, Raftery AE. 2016. mclust 5: Clustering, classification and density estimation using Gaussian finite mixture models. The R Journal 8: 289–317.

Wickham H. 2016. ggplot2: Elegant graphics for data analysis. Springer-Verlag New York.

Wickham H, Averick M, Bryan J, et al. 2019. Welcome to the tidyverse. Journal of Open Source Software 4: 1686.

Wilkinson L. 2005. The grammar of graphics (statistics and computing). Berlin, Heidelberg: Springer-Verlag.

Thank you!

jamesotto852.github.io/JSM-2022

Additional Materials